一．概念描述

现代数学：中位数和众数都是统计学名词。中位数也称中数，统计学中反映样本集中趋势的统计量。众数是指是一组数据中出现次数最多的数据。

小学数学：小学数学教材对于中位数的概念通常是采取描述式的方式进行的，形如“3.5是这组数据的中位数”。并且教材会明确中位数的优点是不受偏大或偏小数据的影响，因此有时用它代表全体数据的一般水平更合适。

对于众数的概念和中位数的描述方式相同，即形如“1. 52在这组数据中出现的次数最多，是这组数据的众数”。同时，教材会指明：众数能反映一组数据的集中情况。

二．概念解读

(1)中位数和众数的特点

中位数反映了一组数的一般情况。从中位数的定义可知，所研究的数据中有一半小于中位数，一半大于中位数。中位数和众数不同，中位数不一定在这组数据中。 它的作用与算术平均数相近，也是作为所研究数据的代表值。在一个等差数列或一个正态分布数列中，中位数就等于算术平均数。在数列中出现了极端变量值的情况下，用中位数作为代表值要比用算术平均数更好，因为中位数不受极端变量值的影响；如果研究目的就是为了反映中间水平，当然也应该用中位数。在对统计数据进行处理和分析时，可结合中位数的使用。概括地说，中位数特别适合以下情形：一组数据中有特大或特小的极端数据；一组数据中有个别数据不确切；资料属于等级性质。当然中位数也有一定的局限性，如有些离散型变量的单项式数列，当次数分布偏态时，中位数的代表性会受到影响。另外，由于中位数只是数列中的一个局部，因此缺乏敏感性。

众数相对于平均数和中位数这两个集中量是最差的一个。但是在以下情况下，它的使用具有一定的优势：当需要快速而粗略地找出一组数据的代表值时；当需要利用算术平均数、中位数和众数三者之间的关系来粗略判断频数分布的形态时；当需要帮助分析解释一组频数分布是否确实具有两个频数最多的集中点时。

(2)中位数和众数的计算方法

中位数的计算方法可以概括为：当变量值的项数N为奇数时，处于中间位置的变量值即为中位数；当N为偶数时，中位数则为处于中间位置的2个变量值的平均数。需要注意的是，在计算中位数前要将数列进行从小到大或者从大到小的重新排列，而不是随意乱排。

众数是一组数据中最多的，众数可以不存在或存在多个。

三．教学建议

(1)在现实情境中感受中位数、众数的价值

教材将平均数、中位数和众数单独编排，但是分析教材的编写意图可以看到，对于中位数和众数的教学是建立在整体把握的基础上，没有单方面强调某个统计量的优劣。因此，关于中位数和中位数的教学，要通过解决具体问题并在和平均数对比的基础上展开教学。我们首先看一个案例：

小冬的爸爸要到两家公司应聘，哪家的待遇比较高呢？老师呈现了两家公司的信息：

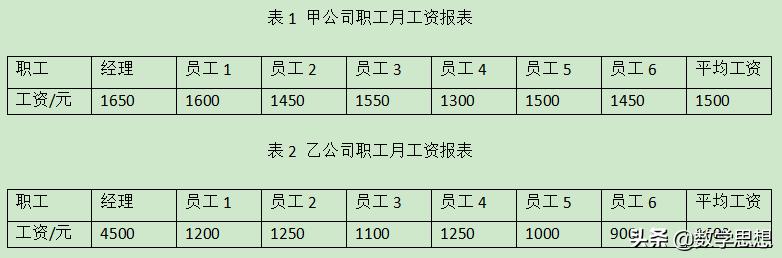
看了这两份工资报表后，你对小冬的爸爸去哪个公司应聘有什么建议？为什么？

在讨论的过程中，学生一开始都认为去乙公司，理由是乙公司的人均工资高。但是随着讨论的深入，学生们开始注意到这些数据的特点。乙公司平均工资高的原因是因为经理的工资远远高于员工的工资，而甲公司虽然整体平均工资低，但是无论是经理还是员工的工资都比较接近。因此，学生逐步认识到平均数在这里不能作为数据的代表了，引出中位数和众数的概念也就成为必然。这样的情境不仅使学生认识了中位数和众数，更重要的是让学生客观认识到它们的价值以及如何应用。

(2)将平均数、中位数和众数的统计意义作为重点

平均数、中位数和众数是在统计与概率领域的重要内容，教学时要充分发挥其在统计分析中的作用。有的老师在教学时将如何计算平均数和中位数、众数作为重点，让学生进行机械的练习。面对枯燥的数据，学生盲目地计算，并不知道计算的意义是什么，这些知识有什么价值。因此，建议教学这些内容时一定加强学生的交流和分析，重在让他们理解统计的意义。另外，由于教材编排的原因，平均数、中位数和众数教学分散，因此我们经常会看到有的课堂学习平均数时教师单一强调平均数的意义，而在学习中位数和众数时又抛开平均数，造成学生对于这些知识理解不够全面，从而使学生往往会孤立地看待这几个概念。因此，对于平均数、中位数和众数意义的理解要建立在整体把握的基础上，同时在解决实际问题中深化理解。